Java多线程和并发面试题（附答案）第6题

6、ConcurrentSkipListMap非阻塞Hash跳表集合？

大家都是知道TreeMap，它是使用树形结构的方式进行存储数据的线程不安全的Map集合（有序的哈希表），并且可以对Map中的Key进行排序，Key中存储的数据需要实现Comparator接口或使用CompareAble接口的子类来实现排序。

ConcurrentSkipListMap也是和TreeMap，它们都是有序的哈希表。但是，它们是有区别的：

● 第一，它们的线程安全机制不同，TreeMap是非线程安全的，而ConcurrentSkipListMap是线程安全的。

● 第二，ConcurrentSkipListMap是通过跳表实现的，而TreeMap是通过红黑树实现的。

● 那现在我们需要知道什么是跳表？

Skip list(跳表）是一种可以代替平衡树的数据结构，默认是按照Key值升序的。Skip list让已排序的数据分布在多层链表中，以0-1随机数决定一个数据的向上攀升与否，通过“空间来换取时间”的一个算法，在每个节点中增加了向前的指针，在插入、删除、查找时可以忽略一些不可能涉及到的结点，从而提高了效率。

从概率上保持数据结构的平衡比显式的保持数据结构平衡要简单的多。对于大多数应用，用Skip list要比用树算法相对简单。由于Skip list比较简单，实现起来会比较容易，虽然和平衡树有着相同的时间复杂度O(log(n))，但是Skip list的常数项会相对小很多。Skip list在空间上也比较节省。一个节点平均只需要1.333个指针（甚至更少）。下图为Skip list结构图

（以7，14，21，32，37，71，85序列为例）。

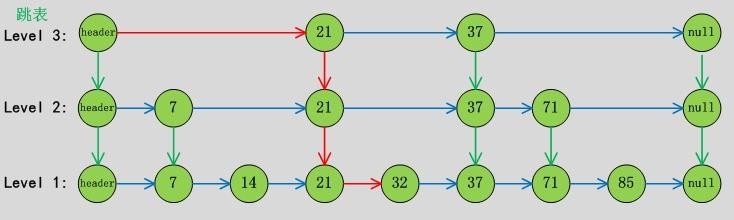
● SkipList性质

● 由很多层结构组成，level是通过一定的概率随机产生的。

● 每一层都是一个有序的链表，默认是升序，也可以根据创建映射时所提供的Comparator进行排序，具体取决于使用的构造方法。

● 最底层（Level 1）的链表包含所有元素。

● 如果一个元素出现在Level i的链表中，则它在Level i之下的链表也都会出现。

● 每个节点包含两个指针，一个指向同一链表中的下一个元素，一个指向下面一层的元素。

● 什么是ConcurrentSkipListMap？

ConcurrentSkipListMap提供了一种线程安全的并发访问的排序映射表。内部是SkipList（跳表）结构实现，在理论上能够在O(log(n))时间内完成查找、插入、删除操作。

注意：调用ConcurrentSkipListMap的size时，由于多个线程可以同时对映射表进行操作，所以映射表需要遍历整个链表才能返回元素个数，这个操作是个O(log(n))的操作。

● ConcurrentSkipListMap 的数据结构，如下图所示：

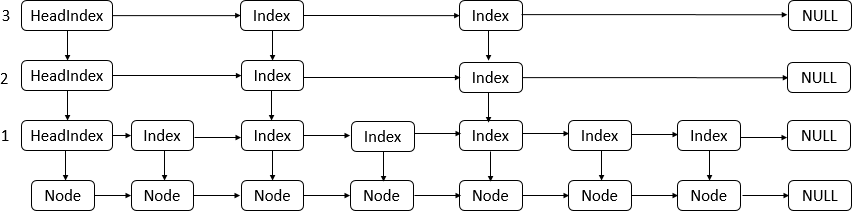
说明：可以看到ConcurrentSkipListMap的数据结构使用的是跳表，每一个HeadIndex、Index结点都会包含一个对Node的引用，同一垂直方向上的Index、HeadIndex结点都包含了最底层的Node结点的引用。并且层级越高，该层级的结点（HeadIndex和Index）数越少。Node结点之间使用单链表结构。

● ConcurrentSkipListMap源码分析

ConcurrentSkipListMap主要用到了Node和Index两种节点的存储方式，通过volatile关键字实现了并发的操作

static final class Node<K, V> {
    final K key;
    volatile Object value;//value 值
    volatile Node<K, V> next;//next 引用
……
}

static class Index<K, V> {
    final Node<K, V> node;
    final Index<K, V> down;//downy 引用
    volatile Index<K, V> right;//右边引用
……
}

● ConcurrentSkipListMap查找操作

通过SkipList的方式进行查找操作：（下图以“查找91”进行说明：）

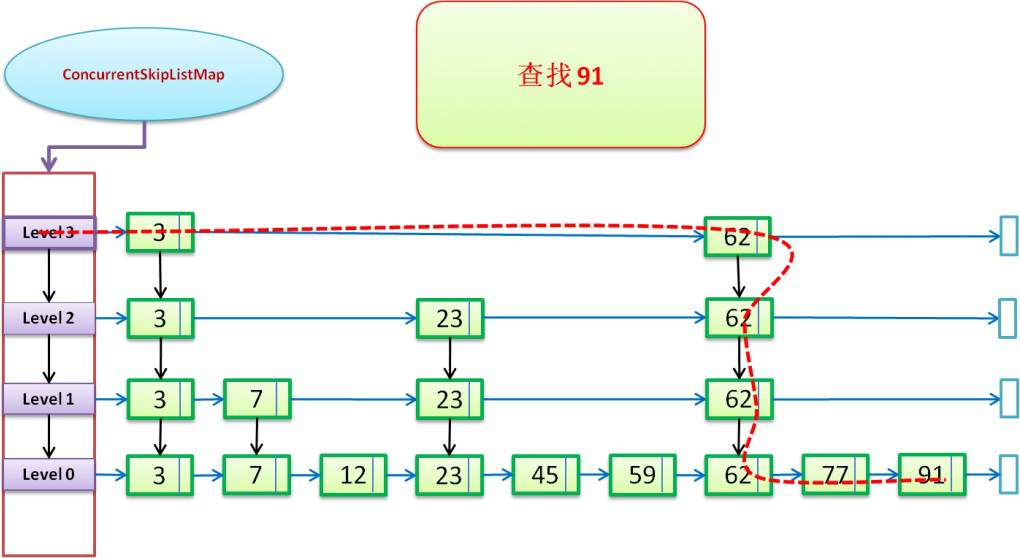
红色虚线，表示查找的路径，蓝色向右箭头表示right引用；黑色向下箭头表示down引用；下面就是源码中的实现（get方法是通过doGet方法来时实现的）。

private V doGet(Object okey) {
    Comparable<? super K> key = comparable(okey);
    for (; ; ) {
        // 找到“key对应的节点”
        Node<K, V> n = findNode(key);
        if (n == null)
            return null;
        Object v = n.value;
        if (v != null)
            return (V) v;
    }
}

● ConcurrentSkipListMap删除操作

通过SkipList的方式进行删除操作：（下图以“删除23”进行说明：）。

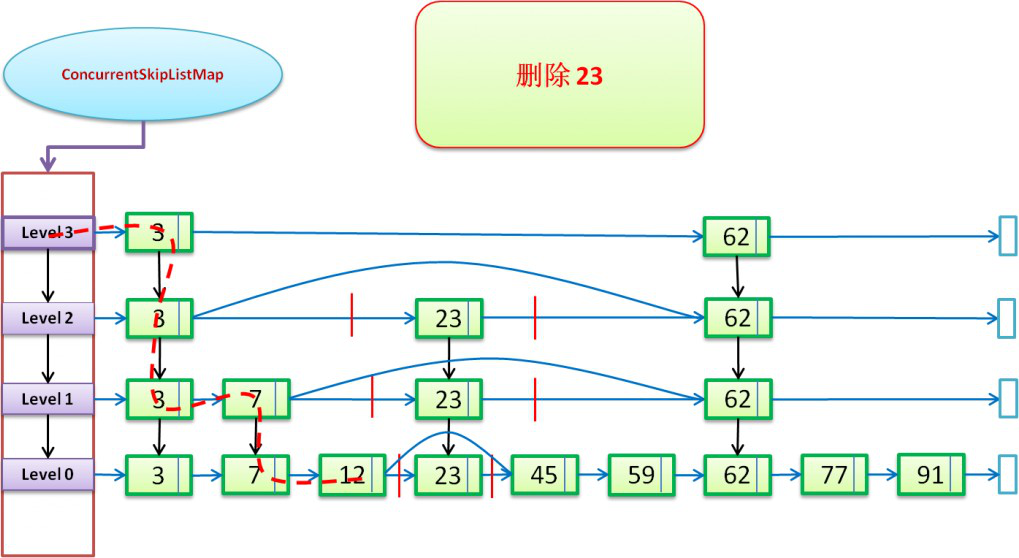
红色虚线，表示查找的路径，蓝色向右箭头表示right引用；黑色向下箭头表示down引用；下面就是源码中的实现（remove方法是通过doRemove方法来时实现的）。

//remove 操作,通过 doRemove 实现,把所有 level 中出现关键字 key 的地方都 delete 掉
public V remove(Object key) {
    return doRemove(key, null);
}

final V doRemove(Object okey, Object value) {
    Comparable<? super K> key = comparable(okey);
    for (; ; ) {
        Node<K, V> b = findPredecessor(key);//得到 key 的前驱（就是比 key 小的最大节点）
        Node<K, V> n = b.next;//前驱节点的 next 引用
        for (; ; ) {//遍历
            if (n == null)//如果 next 引用为空,直接返回
                return null;
            Node<K, V> f = n.next;
            if (n != b.next)    // 如果两次获得的 b.next 不是相同的 Node,就跳转到第一层循环重新获得 b 和 n
                break;
            Object v = n.value;
            if (v == null) {    // 当 n 被其他线程 delete 的时候,其 value==null, 此时做辅助处理,并重新获取 b 和 n
                n.helpDelete(b, f);
                break;
            }
            if (v == n || b.value == null)    // 当其前驱被 delet 的时候直接跳出,重新获取 b 和 n break;
                int c = key.compareTo(n.key);
            if (c < 0)
                return null;
            if (c > 0) {//当 key 较大时就继续遍历
                b = n;
                n = f;
                continue;
            }
            if (value != null && !value.equals(v)) return null;
            if (!n.casValue(v, null)) break;
            if (!n.appendMarker(f) || !b.casNext(n, f))//casNext 方法就是通过比较和设置 b（前驱）的 next 节点的方式来实现删除操作
                findNode(key);    // 通过尝试 findNode 的方式继续 find
            else {
                findPredecessor(key);    // Clean index
                if (head.right == null)    //如果 head 的 right 引用为空,则表示不存在该 level
                    tryReduceLevel();
            }
            return (V) v;
        }
    }
}

● ConcurrentSkipListMap插入操作

通过SkipList的方式进行插入操作：（下图以“添加55”的两种情况，进行说明：）。

 

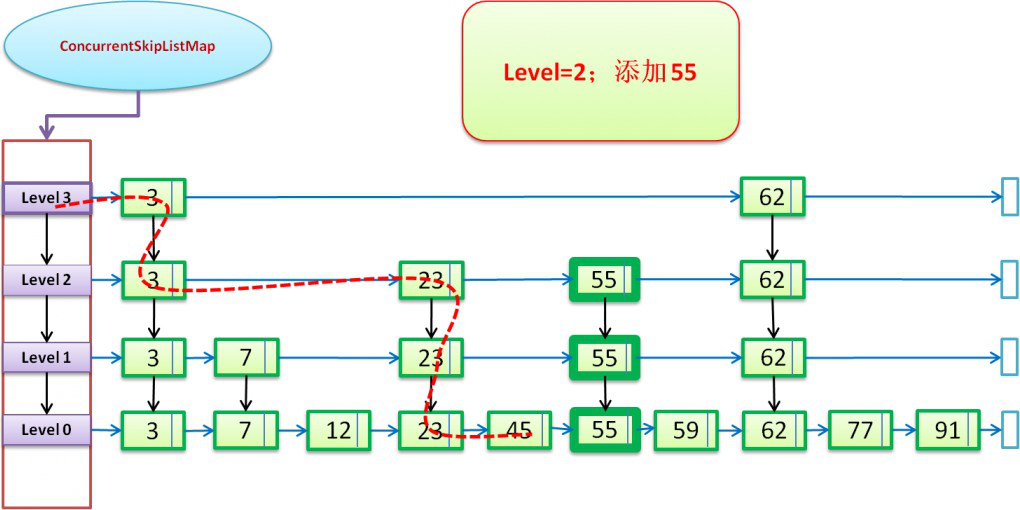
在level=2（该level存在）的情况下添加55的图示:只需在level<=2的合适位置插入55即可在level=4(该level不存在，图示level4是新建的)的情况下添加55的情况：首先新建level4，然后在level<=4的合适位置插入55。

下面就是源码中的实现（put方法是通过doPut方法来时实现的）。

/put 操作,通过 doPut 实现
    public V put(K key, V value) {
        if (value == null)
            throw new NullPointerException();
        return doPut(key, value, false);
    }

    private V doPut(K kkey, V value, boolean onlyIfAbsent) {
        Comparable<? super K> key = comparable(kkey);
        for (; ; ) {
            Node<K, V> b = findPredecessor(key);//前驱
            Node<K, V> n = b.next;
            //定位的过程就是和 get 操作相似
            for (; ; ) {
                if (n != null) {
                    Node<K, V> f = n.next;
                    if (n != b.next) // 前后值不一致的情况下,跳转到第一层循环重新获得 b 和 n
                        break;
                    Object v = n.value;
                    if (v == null) {    // n 被 delete 的情况下
                        n.helpDelete(b, f);
                        break;
                    }
                    if (v == n || b.value == null) // b 被 delete 的情况,重新获取 b 和 n
                        break;
                    int c = key.compareTo(n.key);
                    if (c > 0) {
                        b = n;
                        n = f;
                        continue;
                    }
                    if (c == 0) {
                        if (onlyIfAbsent || n.casValue(v, value)) return (V) v;
                        else
                            break; // restart if lost race to replace value
                    }
                    // else c < 0; fall through
                }
                Node<K, V> z = new Node<K, V>(kkey, value, n);
                if (!b.casNext(n, z))
                    break;    // restart if lost race to append to b
                int level = randomLevel();//得到一个随机的 level 作为该 key-value 插入的最高 level
                if (level > 0)
                    insertIndex(z, level);//进行插入操作
                return null;
            }
        }
    }

    /**
     * 获得一个随机的 level 值
     */
    private int randomLevel() {

        int x = randomSeed;
        x ^= x << 13;
        x ^= x >>> 17;
        randomSeed = x ^= x << 5;
        if ((x & 0x8001) != 0) // test highest and lowest bits
            return 0;
        int level = 1;
        while (((x >>>= 1) & 1) != 0) ++level;
        return level;
    }

    //执行插入操作：如上图所示,有两种可能的情况：
//1.当 level 存在时,对 level<=n 都执行 insert 操作
//2.当 level 不存在（大于目前的最大 level）时,首先添加新的 level,然后在执行操作 1
    private void insertIndex(Node<K, V> z, int level) {
        HeadIndex<K, V> h = head;
        int max = h.level;
        if (level <= max) {//情况 1
            Index<K, V> idx = null;
            for (int i = 1; i <= level; ++i)//首先得到一个包含 1~level 个级别的 down 关系的链表, 最后的 inx 为最高 level
                idx = new Index<K, V>(z, idx, null);
            addIndex(idx, h, level);//把最高 level 的 idx 传给 addIndex 方法
        } else { // 情况 2 增加一个新的级别
            level = max + 1;
            Index<K, V>[] idxs = (Index<K, V>[]) new Index[level + 1];
            Index<K, V> idx = null;
            for (int i = 1; i <= level; ++i)//该步骤和情况 1 类似
                idxs[i] = idx = new Index<K, V>(z, idx, null);
            HeadIndex<K, V> oldh;
            int k;
            for (; ; ) {
                oldh = head;
                int oldLevel = oldh.level;
                if (level <= oldLevel) { // lost race to add level
                    k = level;
                    break;
                }
                HeadIndex<K, V> newh = oldh;
                Node<K, V> oldbase = oldh.node;
                for (int j = oldLevel + 1; j <= level; ++j)
                    newh = new HeadIndex<K, V>(oldbase, newh, idxs[j], j);//创建新的
                if (casHead(oldh, newh)) {
                    k = oldLevel;
                    break;
                }
            }
            addIndex(idxs[k], oldh, k);
        }

    }

    /**
     * 在 1~indexlevel 层中插入数据
     */
    private void addIndex(Index<K, V> idx, HeadIndex<K, V> h, int indexLevel) {
        // insertionLevel 代表要插入的 level,该值会在 indexLevel~1 间遍历一遍
        int insertionLevel = indexLevel;
        Comparable<? super K> key = comparable(idx.node.key);
        if (key == null) throw new NullPointerException();
        // 和 get 操作类似,不同的就是查找的同时在各个 level 上加入了对应的 key
        for (; ; ) {
            int j = h.level;
            Index<K, V> q = h;
            Index<K, V> r = q.right;
            Index<K, V> t = idx;
            for (; ; ) {
                if (r != null) {
                    Node<K, V> n = r.node;
                    // compare before deletion check avoids needing recheck
                    int c = key.compareTo(n.key);
                    if (n.value == null) {
                        if (!q.unlink(r))
                            break;
                        r = q.right;
                        continue;
                    }
                    if (c > 0) {
                        q = r;
                        r = r.right;
                        continue;
                    }
                }
                if (j == insertionLevel) {//在该层 level 中执行插入操作
                    // Don't insert index if node already deleted
                    if (t.indexesDeletedNode()) {
                        findNode(key); // cleans up
                        return;
                    }
                    if (!q.link(r, t))//执行 link 操作,其实就是 inset 的实现部分
                        break; // restart
                    if (--insertionLevel == 0) {
                        // need final deletion check before return
                        if (t.indexesDeletedNode())
                            findNode(key);
                        return;
                    }
                }
                if (--j >= insertionLevel && j < indexLevel)//key 移动到下一层 level
                    t = t.down;
                q = q.down;
                r = q.right;
            }
        }
    }